Anda memilih hadiah dengan hati-hati. Anda sudah menyiapkan gunting, selotip, dan bahkan gulungan kertas bertema Natal.
Namun, bagi kebanyakan dari kita yang bukan ahli dalam membungkus kado, kemungkinan besar hasil akhirnya adalah pembungkusan yang kacau, kertas dan selotip yang campur aduk.
Mungkin itulah sebabnya membungkus kado Natal biasanya bukan tugas yang disukai banyak orang.
Namun tahun ini Anda mungkin ingin menambahkan penggaris dan kalkulator ke perlengkapan pembungkus kado Anda. Saatnya menerapkan kekuatan matematika pada Natal ini.
Berpikirlah secara inovatif
Mungkin barang yang paling mudah untuk dibungkus adalah kotak kubik. Namun banyak dari kita merasa kesulitan untuk memotong jumlah kertas yang tepat untuk menutupi bentuk sederhana ini.
Kadang-kadang kita mempunyai banyak kertas tersisa, yang akhirnya kita lipat sembarangan di bagian ujungnya, atau kita kekurangan kertas dan perlu berimprovisasi dengan potongan kertas tambahan untuk menutupinya seluruhnya.
Namun, ada rumus cerdik yang dikembangkan oleh Sara Santos, ahli matematika di King’s College London, yang tidak hanya membantu mengurangi limbah kertas, tetapi juga mencocokkan pola pada jahitannya.
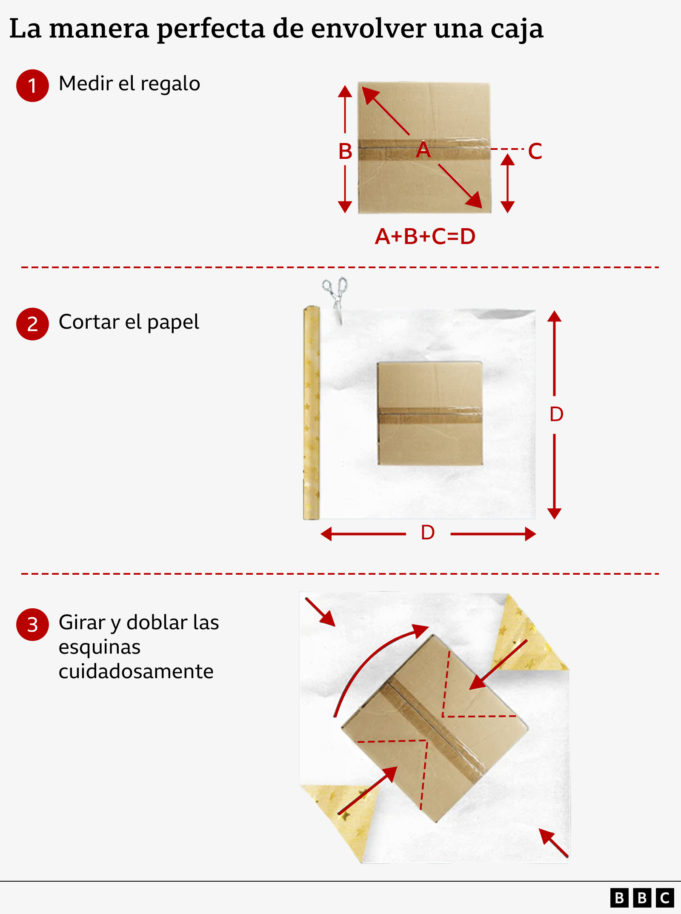
Pertama, Anda harus mengukur tinggi kotak dan mengalikannya dengan 1,5. Selanjutnya, ukur diagonal sisi terbesar kotak, dari sudut ke sudut, dan jumlahkan kedua pengukuran tersebut. Ini memberikan dimensi persegi kertas kado yang perlu dipotong.
Misalnya, jika Anda akan membungkus sebuah kubus berukuran diagonal 4,5 sentimeter dan tinggi 3 cm, maka Anda harus memotong kertas berbentuk persegi berukuran 9 cm x 9 cm. Tapi inilah triknya…
Saat Anda meletakkan kado di atas kertas, Anda harus memutarnya agar berada secara diagonal di tengahnya. Kemudian, lipat keempat sudut kertas dengan hati-hati ke arah tengah, selipkan penutup setiap sudut kotak di bawah sudut yang lebih besar saat Anda melipatnya.
Penting untuk mengamankan kertas hanya dengan tiga selotip kecil, dan jika menggunakan kertas bergaris, pola jahitannya mungkin sama.
Metode ini terkadang juga dapat digunakan untuk parallelepipeds.
“Namun, jika kertasnya berbentuk persegi, tidak selalu benar bahwa kertas yang dibungkus secara diagonal lebih baik,” kata Holly Krieger, profesor matematika di Universitas Cambridge.
Jelaskan, misalnya, bahwa jika sebuah kotak berukuran 2 x 4 x 8 cm, metode diagonal memerlukan kertas persegi berukuran 14 x 14 cm, namun dimungkinkan untuk membungkus kado yang sama secara lebih konvensional dengan kertas persegi berukuran 12 cm.
Trik posisi diagonal lebih berguna jika Anda memiliki selembar kertas persegi yang tidak menutupi kubus biasa.
Dengan menempatkannya secara diagonal, kado dapat ditutupi. Demikian pula, kertas persegi panjang yang tidak seluruhnya menutupi kado berbentuk paralelepiped, seperti kotak sepatu, dapat diakomodasi dengan menempatkan kotak secara diagonal.
Solusi praktis
Metode ini terkadang juga bisa digunakan untuk prisma segitiga.
Ketinggian segitiga di ujung kemasan prisma diukur, digandakan, dan ditambahkan ke total panjang kotak untuk mendapatkan ukuran kertas sempurna yang diperlukan untuk menutupi ujung segitiganya dengan tiga lapis kertas untuk hasil akhir yang sempurna.
Untuk membungkus tabung permen atau kado berbentuk silinder lainnya dengan sedikit limbah kertas, ukur diameter ujung lingkarannya dan kalikan dengan Pi (3,14…) untuk menghitung jumlah kertas yang dibutuhkan untuk membungkus kado.
Selanjutnya, Anda mengukur panjang tabung dan menjumlahkan diameter lingkaran untuk menghitung panjang minimum kertas yang dibutuhkan.
Dengan cara ini, kertas akan bertemu tepat di tengah setiap ujung melingkar kado, sehingga hanya memerlukan selotip kecil untuk mengencangkannya.
Namun, sebaiknya sisakan sedikit kertas tambahan untuk memastikan bentuknya tertutup seluruhnya dan agar kejutannya tidak rusak.

Kembali ke topik…
Jika hadiahnya berupa bola, sial! Tidak diragukan lagi, bola adalah bentuk yang paling sulit untuk dibungkus.
Tidak mungkin menutupi bola secara merata dengan selembar kertas, bukan hanya karena sifat kertas mencegahnya menekuk tanpa batas, tetapi juga karena teorema bola berbulu, jelas Sophie Maclean, seorang pemopuler matematika dan mahasiswa doktoral di King’s College London.
Teorema ini menjelaskan bahwa tidak mungkin menyisir rambut bola atau bola agar lurus tanpa menimbulkan setidaknya satu helai rambut yang berputar-putar atau sulit diatur.
“Jika Anda berpikir untuk membungkus bola dengan kertas kado, Anda tidak akan bisa membuatnya rata seluruhnya,” kata Maclean. “Suatu saat akan ada gumpalan atau lubang.”
“Secara pribadi, saya suka berkreasi saat membungkus kado, dan dalam hal ini saya akan memanfaatkannya. Ikat busur di sekelilingnya atau putar kertasnya agar terlihat seperti permen atau kado berbentuk permen.”
Jika Anda ingin mendapatkan efisiensi maksimal saat membungkus bola sepak dengan kertas, Anda bisa mencoba menggunakan aluminium foil berbentuk segitiga.
Sebuah tim ilmuwan internasional mempelajari cara efisien membungkus coklat Mozartkugel—bola marzipan berlapis praline yang dicelupkan ke dalam coklat hitam—dengan sepotong kecil aluminium foil.
Mereka mengamati bahwa meminimalkan keliling suatu bentuk akan mengurangi pemborosan, sehingga membuat persegi lebih efisien dibandingkan persegi panjang dengan luas yang sama.

Membuat bentuk kelopak adalah cara lain untuk menutupi bola secara efisien, meskipun diperlukan jumlah kelopak yang tidak terbatas untuk melakukannya dengan presisi penuh.
Namun, para peneliti menemukan bahwa pembungkus berbentuk segitiga sama sisi bahkan lebih efisien. “Penghematan sebesar 0,1% dari area tersebut dapat menjadi signifikan bagi jutaan coklat Mozartkugel yang dikonsumsi setiap tahunnya.”
Mereka menambahkan bahwa mungkin ada pengurangan 20% pada material yang dibutuhkan untuk menutupi bentuk bola.
Kita semua mungkin pernah kesulitan membungkus kado yang keras dan tidak beraturan, seperti mug, yang berbentuk silinder terbuka dengan pegangan mencuat.
“Tidak ada rumus matematika pasti yang bisa mendeskripsikan semua bentuk yang mungkin. Ini adalah salah satu situasi di mana eksperimen hampir lebih berguna daripada mencoba mendeskripsikannya secara matematis,” kata Krieger.
Salah satu solusinya adalah dengan menggabungkan satu kado yang bentuknya sulit dengan kado lainnya untuk menciptakan bentuk yang lebih teratur dan lebih mudah untuk dibungkus.

Efisiensi maksimum tanpa menghemat sumber daya
Membungkus dua kado berukuran serupa lebih efisien dibandingkan membungkusnya secara terpisah, karena memerlukan lebih sedikit kertas. Namun membungkus dua kado dengan bentuk atau ukuran yang sangat berbeda biasanya membutuhkan lebih banyak kertas, menurut Krieger.
Dibutuhkan kesabaran dan banyak trial and error saat mengelompokkan bentuk. Bahkan ahli matematika pun mengalami kesulitan.
Beberapa “masalah pengepakan”, seperti menemukan cara paling efisien untuk mengemas persegi identik ke dalam persegi atau persegi panjang yang lebih besar, dikenal sebagai masalah “NP-hard”, yang berarti masalah tersebut sangat sulit atau bahkan hampir mustahil untuk diselesaikan, bahkan dengan komputer paling canggih sekalipun.
Ini adalah bidang penelitian yang sangat aktif di kalangan akademisi.

Menata bola sedemikian rupa sehingga hanya memakan ruang sesedikit mungkin adalah tugas yang sangat sulit, jadi tidak mengherankan jika kita kesulitan membungkus sekantong bola golf dengan efisien.
Untungnya, para ahli matematika sedang mengatasi masalah ini dan mencari cara terbaik untuk melakukannya.
Namun, bagi mereka yang berpikiran jernih, solusi terbaik hingga saat ini tampaknya memerlukan metode pengemasan yang tidak terstruktur dan cukup acak, serta beberapa perhitungan yang luar biasa.
Mempraktikkan metode Santos dapat menghemat kertas dan selotip serta mengesankan keluarga dan teman Anda, namun terkadang ahli matematika pun tergoda untuk mengambil jalan pintas saat dihadapkan pada pembungkus kado yang sangat rumit, seperti bola.
“Mungkin saya akan membeli sekotak saja,” canda Krieger.
Teruslah membaca:
* 3 langkah menghindari bencana saat membuka kado natal
* 5 aksesoris teknologi untuk diberikan kepada orang tua pada Natal ini
* Bagaimana memberi hadiah kepada orang yang Anda cintai dan menghindari hal-hal yang berlebihan di hari Natal

klik disini untuk membaca lebih banyak cerita dari BBC News Mundo.
Berlangganan di sini ke buletin baru kami untuk menerima pilihan konten terbaik minggu ini setiap hari Jumat.
Anda juga dapat mengikuti kami YouTube, Instagram, TikTok, X, Facebook dan di kami yang baru saluran whatsapptempat Anda akan menemukan berita terkini dan konten terbaik kami.
Dan ingat bahwa Anda dapat menerima notifikasi di aplikasi kami. Unduh versi terbaru dan aktifkan.